
In particular, method 'b' seems a bit more efficient, since it employs one less subarea, compared to method 'c'. For each one of their subareas, there are easily available analytical formulas, we can use to calculate their moments of inertia around a parallel to global axis. Methods 'b' and 'c' on the other hand, do not present such a problem. Surely, it can be done this way, but it is not very efficient calculation wise. Firstly, we have to find the moments of inertia I x and I y around the inclined centroidal axes of the rectangle, and then transform them around a horizontal axis, using the formulas for axis rotation. No formula is available for this particular angle of inclination of the rectangle that gives its moment of inertia around an axis parallel to the global one. Method 'a' seems more simple, and employs the least number of subareas, but the calculation of the moment of inertia of the central inclined rectangle is rather hard. Three alternative ways to divide the top-left gray area to subareas, in order to find its moment of inertia around a horizontal axis. With method 'a', the number of subareas is 4, with method 'b' it is 5 and and with method 'c', 6. The global axis of rotation is indicated with red dashed line. The following picture demonstrates a case of a composite area, that is decomposed to smaller subareas, using three different methods (among many others possible). Efficiency is important, because sometimes there are many ways to decompose an area, but not all of them are equally easy for calculations. While doing so, we must ensure that we can efficiently obtain the moment inertia of each subarea, around a parallel axis. With step 1 we aim to divide the complex area under investigation to smaller and more manageable subareas. Flowchart for the calculation of the moment of inertia of a composite area Add (or subtract for negative subareas, see examples) the moments of inertia from the last step.įigure 1.Apply the Parallel Axes Theorem to find the moment of inertia of each subarea around the global axis.Determine the moment of inertia of each subarea, around a parallel axis, passing through subarea centroid.Determine the distance from global axis of the centroid of each one of the subareas.Identify simply shaped subareas the composite area can be decomposed to.In general, the steps for the calculation of the moment of inertia of a composite area, around an axis (called global axis hereafter), are summarized to the following:
Moment of inertia formula for cross section how to#
In this article, it is demonstrated how to calculate the moment of inertia of complex shapes, using the Parallel Axes Theorem.

The possible shape geometries one may encounter however, are unlimited, but most of the times, these complex areas can be decomposed to more simple subareas. For a circular tube section, substitution to the above expression gives the following radius of gyration, around any axis:Ĭircle is the shape with minimum radius of gyration, compared to any other section with the same area A.The given analytical formulas for the calculation of moments of inertia usually cover, just a handful of rather simple cases. Small radius indicates a more compact cross-section. It describes how far from centroid the area is distributed. The dimensions of radius of gyration are. Where I the moment of inertia of the cross-section around a given axis and A its area. Radius of gyration R_g of a cross-section is given by the formula: Where, D, is the outer diameter and D_i, is the inner one, equal to: D_i=D-2t. Įxpressed in terms of diamters, the plastic modulus of the circular tube, is given by the formula: The last formula reveals that the plastic section modulus of the circular tube, is equivalent to the difference between the respective plastic moduli of two solid circles: the external one, with radius R and the internal one, with radius R_i. The moment of inertia (second moment of area) of a circular hollow section, around any axis passing through its centroid, is given by the following expression:

The total circumferences (inner and outer combined) is then found with the formula: Its circumferences, outer and inner, can be found from the respective circumferences of the outer and inner circles of the tubular section.
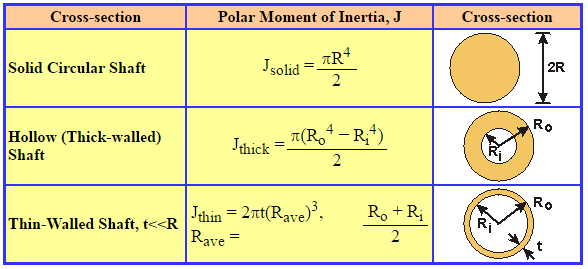
Where D_i=D-2t the inner, hollow area diameter. In terms of tube diameters, the above formula is equivalent to: Where R_i=R-t the inner, hollow area radius. The area A of a circular hollow cross-section, having radius R, and wall thickness t, can be found with the next formula:


 0 kommentar(er)
0 kommentar(er)
